Funciones Exponenciales

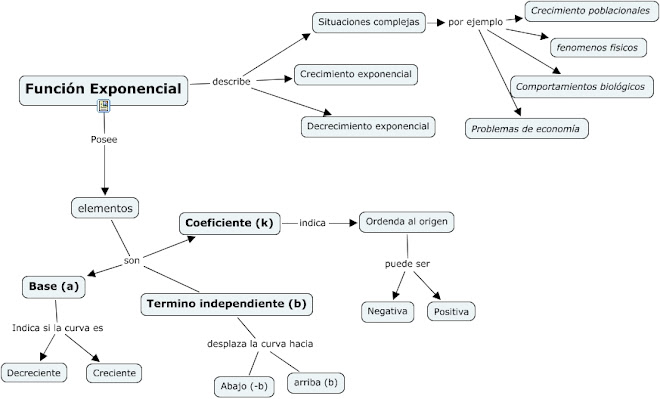
¿Qué es una función exponencial?

Se llaman así a todas aquellas funciones de la forma f(x) = b^x, en donde la base b, es una constante y el exponente la variable independiente. Estas funciones tienen gran aplicación en campos muy diversos como la biología, administración, economía, química, física e ingeniería.

La definición de función exponencial exige que la base sea siempre positiva y diferente de uno (b>0 y b≠1). La condición que b sea diferente de uno se impone, debido a que al reemplazar a b por 1, la función bx se transforma en la función constante f(x) = 1. La base no puede ser negativa porque funciones de la forma f(x)=(-9)1/2 no tendrían sentido en los números reales.


El dominio de la función exponencial está formada por el conjunto de los números reales y su recorrido está representado por el conjunto de los números positivos.

Una situación que nos permite abordar este tema es la siguiente:

Supongamos que un coche que hoy cuesta $10 mil se deprecia de tal forma que cada año que pasa, el valor es el 95% de su valor anterior.
Te pedimos que respondas a las siguientes preguntas: a) ¿Cuál será el valor del auto luego de dos años? ¿Luego de 3 años? b) ¿Cuál será el valor del auto luego de 14 meses?
Podrás observar rápidamente que para obtener el valor del automóvil luego de 10 años deberíamos conocer el valor del año anterior (9), y para éste necesitamos el valor luego de 8 años, etc. Las cuentas se complican.
¿Podremos hallar una fórmula que nos permita obtener directamente el valor luego de x años, sin necesidad de realizar tantas cuentas?

Material extraído de distintas paginas del sitio educar.org